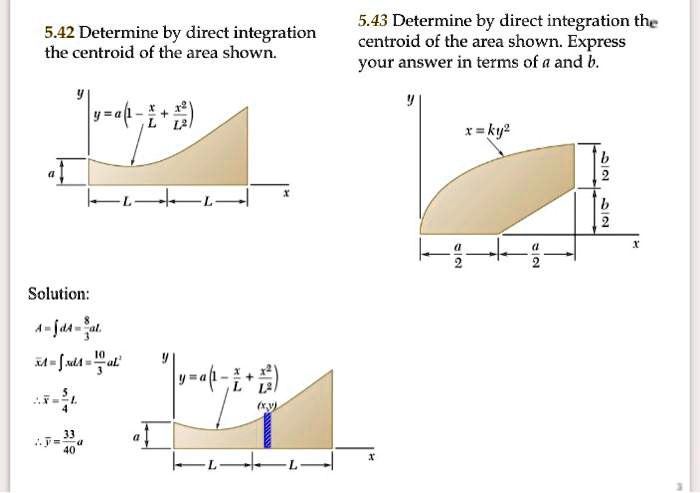
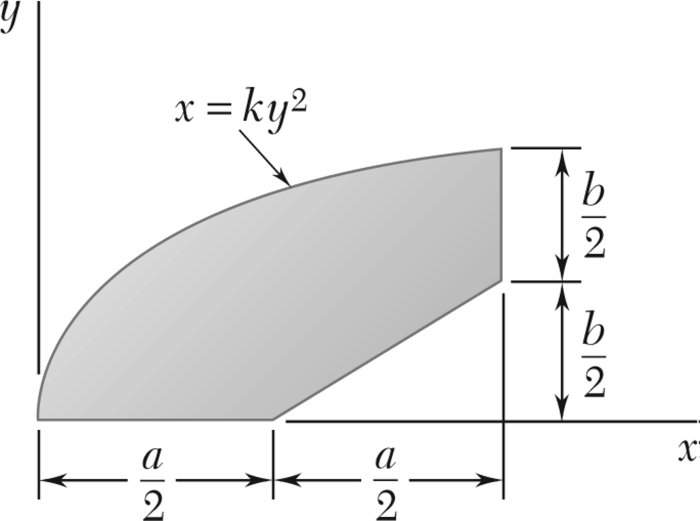
Determine the centroid of the area shown by direct integration – In the realm of geometry, the determination of a figure’s centroid, also known as its geometric center, holds significant importance. Among the various methods employed for centroid calculation, direct integration stands out as a powerful tool. This article delves into the concept of centroid determination through direct integration, exploring its mathematical formulation, integration procedures, geometric applications, and practical implementation.
Direct integration offers a precise and versatile approach to centroid calculation, enabling the analysis of complex shapes with irregular boundaries. By employing this method, we can uncover the centroid’s location, providing valuable insights into the shape’s properties and characteristics.
Overview of Centroid Determination by Direct Integration
The centroid of an area is a geometric concept that represents the center of mass or the average position of the area. It is a significant parameter used to analyze the shape and distribution of an area.
Direct integration is a method for determining the centroid of an area by calculating the first moments of the area with respect to the coordinate axes. It involves dividing the area into small elements, calculating the contribution of each element to the first moments, and then summing up these contributions to obtain the overall centroid.
Mathematical Formulation, Determine the centroid of the area shown by direct integration
The mathematical formula for calculating the centroid of an area using direct integration is given by:
x̄ = (1/A) ∫∫Rx dA
ȳ = (1/A) ∫∫ Ry dA
where:
- x̄, ȳ are the x and y coordinates of the centroid, respectively
- A is the total area of the region R
- x, y are the coordinates of the point in the region R
- dA is the differential area element
Integration Procedures
To perform direct integration for centroid determination, the following steps are involved:
- Divide the area into small elements. The choice of elements depends on the shape of the area.
- Calculate the area of each element.
- Find the x and y coordinates of the centroid of each element.
- Calculate the first moments of each element with respect to the x and y axes.
- Sum up the first moments of all the elements to obtain the overall first moments.
- Divide the overall first moments by the total area to obtain the x and y coordinates of the centroid.
Applications in Geometry
Direct integration for centroid determination finds applications in various geometric shapes, including:
- Rectangles
- Triangles
- Circles
- Ellipses
- Parallelograms
The centroid can be used to analyze the shape’s properties and characteristics, such as its center of mass, symmetry, and moments of inertia.
Implementation in Practice
Direct integration for centroid determination is widely used in practice in fields such as:
- Engineering
- Architecture
- Physics
- Computer graphics
It provides a reliable and accurate method for calculating the centroid of complex shapes with irregular boundaries.
FAQs: Determine The Centroid Of The Area Shown By Direct Integration
What is the significance of centroid determination?
Centroid determination plays a crucial role in understanding the geometric properties of shapes. It provides insights into the shape’s balance, stability, and distribution of mass.
How does direct integration facilitate centroid calculation?
Direct integration involves dividing the area into infinitesimal elements and calculating their individual contributions to the centroid. By integrating these contributions over the entire area, we obtain the coordinates of the centroid.
What are the limitations of using direct integration for centroid determination?
Direct integration may become computationally intensive for complex shapes with intricate boundaries. In such cases, alternative methods like the method of moments or graphical techniques may be more suitable.